等腰三角形证明 中国古建筑岳阳楼简介，它凭啥能与黄鹤楼、滕王阁并称江南三大名楼？

<{股票配资}>等腰三角形证明 中国古建筑岳阳楼简介，它凭啥能与黄鹤楼、滕王阁并称江南三大名楼？

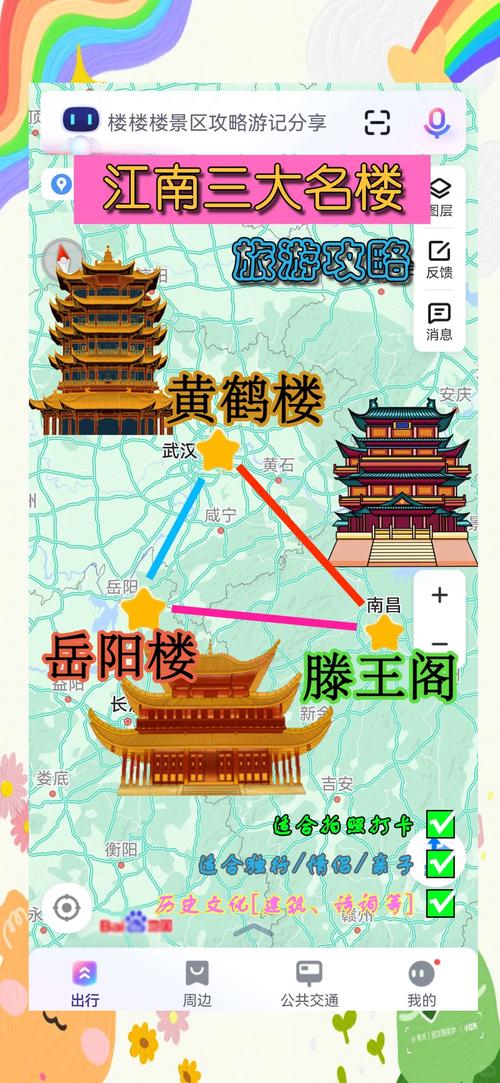
中国古建筑欣赏1岳阳楼简介岳阳楼位于湖南省岳阳市古城西门城墙之上，下瞰洞庭，前望君山，  自古有“洞庭天下水，岳阳天下楼”之美誉，与湖北武昌黄鹤楼、江西南昌滕王阁并称为“江南三大名楼”。1988年1月被国务院确定为全国重点文物保护单位。岳阳楼主楼  高19.42米，进深14.54米，宽17.42  米，为三层、四柱、飞檐、盔顶、纯木结构，整座建筑没用一钉一铆，仅靠木制构件的彼此勾连。  楼中四根楠木金柱直贯楼顶，周围绕以廊、枋、橡、檩互相榫合，结为整体。2提出问题用一个三角形木板和一个重锤组成的工具，就能检查一根横梁是否水平，你知道为什么吗？313.3.1等腰三角形的性质第13章 轴对称4讲授新课等腰三角形的性质1一试一试：拿出桌上的三角形，大家可以通过观察、测量、折叠等方法，看看这个三角形是什么三角形？互动探究CBA5探究三讲授新课等腰三角形的性质1一通过测量，折叠等方法，看看等腰三角形是否是轴对称图形？互动探究CBA探究一作出等腰三角形的顶角平分线、底边上的高、底边上的中线。你有什么发现？猜想2：等腰三角形两底角相等.探究二通过测量，折叠等方法，看看等腰三角形两底角有什么关系？猜想3：等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合.猜想1：等腰三角形是轴对称图形.6总结归纳等腰三角形的性质等腰三角形是轴对称图形，其对称轴是顶角平分线（底边上的中线或者底边上的高）所在直线.性质定理1：等腰三角形的两底角相等.（简写成“等边对等角”）性质定理2：等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合（简写成“三线合一”）7性质2 等腰三角形的顶角平分线，底边上的中线，底边上的高互相重合（通常说成等腰三角形的“三线合一”）.ABCD((12 填一填:根据等腰三角形性质定理2完成下列填空. 在ABC中， AB=AC时， （1）∵AD⊥BC,∴∠_____ = ∠_____，____= ____.(2) ∵AD是中线，∴____⊥____ ，∠_____ =∠_____.(3) ∵AD是角平分线，∴____ ⊥____ ，_____ =_____.三条线段，知一得二练习1、等腰三角形的一个顶角是50°，则这个三角形的底角的大小是50°65°9方法总结：等腰三角形的两个底角相等，已知一个内角等腰三角形证明，则这个角可能是底角也可能是顶角，要分两种情况讨论．练习2：等腰三角形的一个内角是50°，则这个三角形的另外两个内角的大小是50°50°65°、65°或50°、80°10练习3：等腰三角形的一个内角是120°，则这个三角形的另外两个内角的大小是30° 例1 如图，在ABC中 ，AB=AC，点D在AC上，且BD=BC=AD，求ABC各角的度数.12例2、 如图，已知点D、E在ABC的边BC上等腰三角形证明，AB＝AC，AD＝AE.求证：BD＝CE.证明：如图，过A作AG⊥BC于G.∵AB＝AC，AD＝AE，∴BG＝CG，DG＝EG，∴BG－DG＝CG－EG，∴BD＝CE.方法总结：在等腰三角形有关计算或证明中等腰三角形证明 中国古建筑岳阳楼简介，它凭啥能与黄鹤楼、滕王阁并称江南三大名楼？，有时需要添加辅助线，其顶角平分线、底边上的高、底边上的中线是常见的辅助线．G13解决问题14数学来源于生活，又服务于生活！用数学的眼光看世界等腰三角形证明 中国古建筑岳阳楼简介，它凭啥能与黄鹤楼、滕王阁并称江南三大名楼？，你会有意想不到的惊喜！我想对你说：15课堂小结谈一谈：你有什么收获？一个等腰三角形；两个相等；三线合一；三点注意.16等腰三角形的性质等边对等角三线合一注意是指同一个三角形中注意是指顶角的平分线,底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.等腰三角形是轴对称图形注意其对称轴是顶角平分线（底边上的高、底边上的中线）所在直线课堂小结17作业布置1.必做题：作业本上完成书P82 T4 、T6.2.选做题：如图已知点D、E在ABC的边BC上，AB＝AC，BD＝CE，F为DE的中点，求证：AF⊥BC.18$$